| V I S U A L I Z Z A D I S C U S S I O N E |
| GP |
Inserito il - 15 gennaio 2009 : 20:02:11
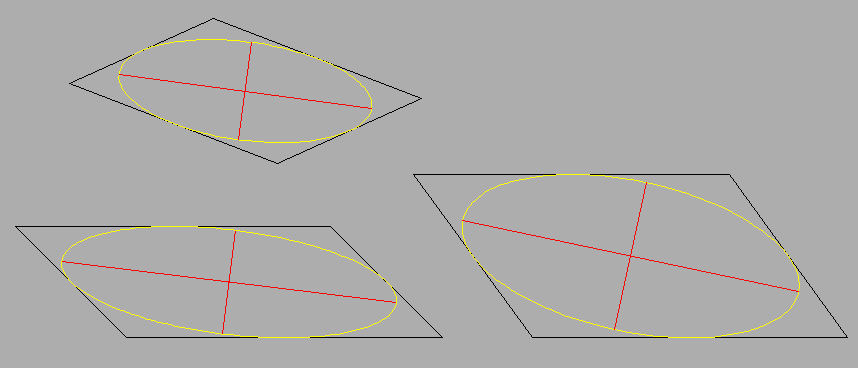
Il lisp disegna un'ellisse inscritta in un parallelogramma selezionando i quattro vertici dello stesso.
Potevano bastare anche tre vertici (o due lati), ma così viene effettuato un controllo per verificare se il poligono sia un "vero" parallelogramma.
Questa la discussione ispiratrice.
Il sorgente:
 ELL4P.zip ELL4P.zip
|
| 7 U L T I M E R I S P O S T E (in alto le più recenti) |
| Giuseppe Mauro |
Inserito il - 14 gennaio 2025 : 10:17:55
Scarica allegato:
 ELL4P.LSP ELL4P.LSP
5,79 KB
Niente. Su estensione LSP da un errore il server, mentre lo ZIP è perfettamente scaricabile.
Scarica allegato:
 ELL4P.zip ELL4P.zip
2,19 KB
Scarica allegato:
 ELL4P_2020.zip ELL4P_2020.zip
2,26 KB
Nella versione 2020 ho sostituito command con command-s per maggiore compatibilita' |
| GP |
Inserito il - 10 gennaio 2025 : 14:47:13
...e niente... sembra proprio impossibile scaricare file dal sito... Peppe, pensaci tu!!! |
| GP |
Inserito il - 10 gennaio 2025 : 14:45:35
Come da richiesta tramite messaggio privato, allego il file del primo post in quanto non risulta più scaricabile.
Ne approfitto per portare un caro saluto all'esimio amministratore 
Scarica allegato:
 ELL4P.LSP ELL4P.LSP
5,71 KB
Scarica allegato:
 ELL4P.zip ELL4P.zip
2,13 KB |
| GP |
Inserito il - 04 febbraio 2009 : 12:12:50
A mo di chiusa riporto l'intervento di MrBoses su treddi per segnalare un ulteriore metodo grafico, ho provato e funziona perfettamente.
Saluti
Io per sgabolare il problema ho fatto così:
usa il comando "arco di ellisse", e dagli come assi le due mediane del parallelogramma che hai ottenuto con le proiezioni. Quindi, ti chiederà l'angolo su cui sviluppare l'arco, traccialo partendo da un punto sulla diagonale del parallelogramma e fai finire l'arco su un'altra diagonale.
il problema è che autocad, non prevedendo la costruzione di ellissi con assi non ortogonali, disegnerà un arco che non passa per i tuoi punti. Semplicemente, prendi i tre punti dell'arco e spostali sui punti della costruzione. ti assicuro che poi unendo i 4 archi reallizzati, otterrai un'ellisse perfetta. Me l'ha confermato il prof. a revisione mercoledì mattina. |
| arri |
Inserito il - 04 febbraio 2009 : 11:16:26
in caso di pulizia forum, questo è una discussione da salvare :) |
| Giuseppe Mauro |
Inserito il - 04 febbraio 2009 : 10:51:53
sempre belle cosine  |
| joseph |
Inserito il - 19 gennaio 2009 : 00:41:13
Aggiungo la costruzione geometrica che sfrutta la relazione fra 2 diametri coniugati qualsiasi e i due assi principali d'inerzia.
Immagine inserita:
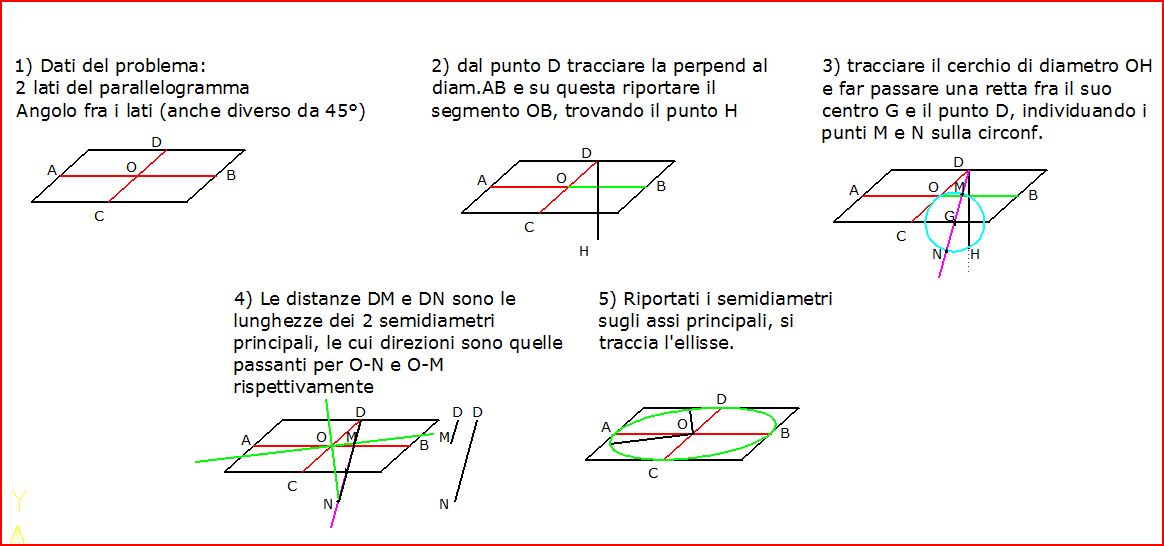
99,51 KB
Buona notte a tutti.
P.S.
Se ne potrebbe anche ricavare, con un po' di pazienza, una soluzione analitica da tradurre in un file LSP. |
